Capacitores
Capacitância de um condutor (C):
É o quociente entre a carga elétrica(Q) cedida ao condutor e o potencial elétrico(Vc) que ele adquire.
C = Q/Vc
Aumentando-se a carga no condutor o potencial por ele adquirido aumenta na mesma proporção, pois a capacitância de um condutor é uma constante ,dependendo somente de sua forma e do meio que o envolve.
Capacitor ou condensador :
É qualquer sistema constituído por dois condutores separados por um dielétrico. Os condutores que fazem parte do capacitor são chamados de armaduras.
Só tem interesse o caso de capacitores cujas armaduras tenham cargas simétricas.
Unidade de medida:
Só tem interesse o caso de capacitores cujas armaduras tenham cargas simétricas.
Unidade de medida:
A unidade de medida do S.I. é o Coulomb/volt. Um nome especial, o Farad(F), foi escolhido para representá-la em homenagem a Michael Faraday(1791- 1867), que, entre outras contribuições, também desenvolveu o conceito de Capacitância.
1 Farad = 1 coulomb / 1 volt
Farad é a capacitância em um elemento passivo em cujos terminais se manifesta uma diferença de potencial de 1 Volt quando carregado com uma carga elétrica de 1 Coulomb.
Por ser uma unidade muito grande, é normalmente utilizado o microfarad(uF), o nanofarad(nF) e o picofarad(pF).
1 uF = 1 F/1.000.000
1 nF = 1 F/1.000.000.000
1 pF = 1 F/1.000.000.000.000
Basicamente o capacitor plano é constituído por duas placas condutoras paralelas(armaduras) separadas por um isolante(dielétrico).
V = Diferença de potencial nos extremos do capacitor em Volts.
Importante observar que a carga elétrica total do sistema é igual a zero.
A Capacitância de um Condensador independe da carga elétrica acumulada ou da tensão elétrica desenvolvida em seus extremos. Sua capacitância é constante, calculada em função de suas dimensões e do dielétrico utilizado.
Fonte: Halliday - Resnick. Física vol. II-1
Símbolo esquemático:
Para t = 5T = 5.R.C temos:
ln(Vcc/(Vcc - Vc)) = 5
Vcc/(Vcc - Vc) = e^5
Vcc = (e^5)(Vcc - Vc)
Vcc = (e^5)Vcc - (e^5)Vc
(e^5)Vc = (e^5)Vcc - Vcc
Vc = Vcc((e^5) - 1)/(e^5)
Vc = Vcc(148,9 - 1)/148,9
Vc = 0,993.Vcc
Vc =(99,3/100).Vcc
Vc = 99,3 % de Vcc.
Para t = 5.R.C a tensão no capacitor é igual a 99,3 % da tensão da bateria.
Só existe corrente elétrica no circuito enquanto o capacitor estiver se carregando. Depois de carregado o capacitor bloqueia a corrente contínua.
Descarga em um capacitor(C) através de um resistor(R)
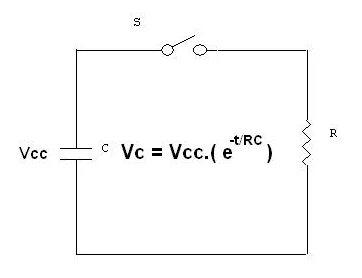
Vc = Vcc.e^(-t/RC)
Vc/Vcc = e^(-t/RC)
1/e^(t/RC) = Vc/Vcc
e^(t/RC) = Vcc/V
Aplicando logarítmo nos dois membros da equação temos:
lne^(t/RC) = ln(Vcc/Vc)
(t/RC).lne = ln(Vcc/Vc)
t/RC = ln(Vcc/Vc)
t = R.C.ln(Vcc/Vc)
t = R.C.ln(Vcc/vc)
Fazendo t = T = R.C temos:
R.C = R.C.ln(Vcc/Vc)
ln(Vcc/Vc) = 1
Vcc/VC = e
Vc/Vcc = 1 / e
e = 2,72
Vc/Vcc = 1/2,72
Vc/Vcc = 0,3676
Vc = (36,8/100).Vcc
Vc = 36,8 % de Vcc.
Para t = R.C, o capacitor perde 63,2 % de sua carga inicial.
Referências Bibliográficas :
Física do Científico e do Vestibular. Vol 5 - Dalton Gonçalves
Física II - 1 - Halliday - Resnick
1 Farad = 1 coulomb / 1 volt
Farad é a capacitância em um elemento passivo em cujos terminais se manifesta uma diferença de potencial de 1 Volt quando carregado com uma carga elétrica de 1 Coulomb.
Por ser uma unidade muito grande, é normalmente utilizado o microfarad(uF), o nanofarad(nF) e o picofarad(pF).
1 uF = 1 F/1.000.000
1 nF = 1 F/1.000.000.000
1 pF = 1 F/1.000.000.000.000
Constante eletrostática, permissividade elétrica e constante dielétrica.
Capacitor Plano:
Capacitância de um capacitor é a razão entre a carga elétrica acumulada em uma de suas armaduras e a diferença de potencial desenvolvida em seus extremos.
C = Q / V
C = Capacitância em Farads
Q = Carga elétrica acumulada em uma das armaduras em Coulombs.V = Diferença de potencial nos extremos do capacitor em Volts.
Importante observar que a carga elétrica total do sistema é igual a zero.
A Capacitância de um Condensador independe da carga elétrica acumulada ou da tensão elétrica desenvolvida em seus extremos. Sua capacitância é constante, calculada em função de suas dimensões e do dielétrico utilizado.
Para cálculo que não exija grande precisão, a permissividade elétrica do ar pode ser considerada igual a do vácuo.
Exemplo:
Queremos construir um condensador plano, de capacidade igual a um farad, usando ar como dielétrico.
As duas armaduras devem ser circulares e separadas por uma distância igual a 1,0 mm.
Qual deve ser o diâmetro de cada placa?
Solução:
O resultado obtido demonstra que o farad é uma unidade muito grande. Na prática,os valores utilizados são da ordem do microfarad, nanofarad e o picofarad.
Capacitor Plano com Dielétrico.
Michael Faraday foi quem primeiro investigou, em 1837, o efeito que se obtém ao preencher o espaço entre as placas com um dielétrico como mica ou óleo. Nas palavras do próprio Faraday :
A pergunta pode ser enunciada da maneira seguinte. Seja A uma placa eletrizada suspensa no ar, B e C duas outras, isoladas, idênticas a A e dela equidistantes, dispostas paralelamente em lados opostos. A placa A estabelecerá uma indução identica sobre B e C(isto é, as cargas que aparecerão nestas placas serão iguais). Se nesta situação, um outro dielétrico diferente do ar, por exemplo goma-laca, for introduzido entre A e C, será que a indução entre estas placas permanece a mesma? Será que a relação de C e B com A permanece inalterada, não obstante a presença do dielétrico introduzido entre elas?
Faraday respondeu esta pergunta construindo dois capacitores idênticos num dos quais foi introduzido um dielétrico, enquanto o outro continha ar a pressão normal. Quando os dois capacitores foram carregados sob a mesma diferença de potencial, Faraday verificou experimentalmente que a carga do capacitor que continha o dielétrico era maior que a do outro.
Faraday mediu a carga relativa nas placas dos dois capacitores tocando-as com uma pequena esfera metálica(segura por um cabo isolante), a qual adquiria uma carga proporcional à existente nos capacitores. Ele então levou esta esfera a uma balança de torção, medindo o valor da repulsão coulombiana sobre outra esfera carregada(padrão) montada no braço da balança.
Uma vez que a presença do dielétrico em C2, veja figura acima, aumenta a carga elétrica acumulada no mesmo e ambos os capacitores(C1 e C2), estão submetidos a mesma diferença de potencial(V), a relação C = Q/V nos mostra que aumenta a capacitância de C2.
A razão entre os valores das capacitâncias, respectivamente com e sem dielétrico , é chamada de constante dielétrica do material
Em vez de manter os dois capacitores com a mesma diferença de potencial(V), também podemos colocar os dois com a mesma carga elétrica(Q).
A experiência mostra que o capacitor com dielétrico desenvolve uma diferença de potencial menor em seus extremos.
Tabela de alguns dielétricos.
Fonte: Halliday - Resnick. Física vol. II-1
Símbolo esquemático:
Carga em um Capacitor(C) através de um resistor(R).
A tensão (Vc) em um capacitor(C) ligado a uma bateria(Vcc) através de um resistor(R) é dada pela expressão:
Vc = Vcc(1- e ^(-t/R.C))
Vc = Vcc - Vcc.e^(-t/RC)
Vcc.e^(-t/R.C) = Vcc - Vc
e^(-t/R.C) = (Vcc - Vc) / Vcc
1 / e^(t/R.C) = (Vcc - Vc)/ Vcc
e^(t/R.C) = Vcc/(Vcc- Vc)
Aplicando logarítmo nos dois membros da equação temos:
ln(e^(t/RC)) = ln(Vcc/(Vcc - Vc))
t/R.C.ln e= ln(Vcc/(Vcc - Vc))
ln e = 1
t/R.C = ln(Vcc/(Vcc - Vc))
t = R.C.ln(Vcc/(Vcc - Vc))
t ... Tempo em segundos após ligar a chave.
Vc...Tensão no capacitor em volts..
Vcc ... Tensão da bateria em volts..
e ... Base do logarítmo neperiano
e = 2,7182818...
Constante de tempo capacitiva (T)
T = R.C
Para t = T = R.C temos:
ln(Vcc/(Vcc - Vc)) = 1
Vcc/(Vcc - Vc) = e
Vcc = e(Vcc - Vc)
Vcc = e.Vcc - e.Vc
eVc = eVcc - Vcc
e.Vc = Vcc(e -1)
Vc = vcc(e - 1)/e
Vc = Vcc(2,72 - 1)/2,72
Vc = 0,632.Vcc
Vc = (63,2/100).Vcc
Vc = 63,2 % de Vcc
Logo, para t = R.C, a tensão no capacitor é igual a 63,2 % da tensão da bateria.
Para t = 5T = 5.R.C temos:
ln(Vcc/(Vcc - Vc)) = 5
Vcc/(Vcc - Vc) = e^5
Vcc = (e^5)(Vcc - Vc)
Vcc = (e^5)Vcc - (e^5)Vc
(e^5)Vc = (e^5)Vcc - Vcc
Vc = Vcc((e^5) - 1)/(e^5)
Vc = Vcc(148,9 - 1)/148,9
Vc = 0,993.Vcc
Vc =(99,3/100).Vcc
Vc = 99,3 % de Vcc.
Para t = 5.R.C a tensão no capacitor é igual a 99,3 % da tensão da bateria.
Só existe corrente elétrica no circuito enquanto o capacitor estiver se carregando. Depois de carregado o capacitor bloqueia a corrente contínua.
Descarga em um capacitor(C) através de um resistor(R)
Vc = Vcc.e^(-t/RC)
Vc/Vcc = e^(-t/RC)
1/e^(t/RC) = Vc/Vcc
e^(t/RC) = Vcc/V
Aplicando logarítmo nos dois membros da equação temos:
lne^(t/RC) = ln(Vcc/Vc)
(t/RC).lne = ln(Vcc/Vc)
t/RC = ln(Vcc/Vc)
t = R.C.ln(Vcc/Vc)
Fazendo t = T = R.C temos:
R.C = R.C.ln(Vcc/Vc)
ln(Vcc/Vc) = 1
Vcc/VC = e
Vc/Vcc = 1 / e
e = 2,72
Vc/Vcc = 1/2,72
Vc/Vcc = 0,3676
Vc = (36,8/100).Vcc
Vc = 36,8 % de Vcc.
Para t = R.C, o capacitor perde 63,2 % de sua carga inicial.
t = R.C.ln( Vcc/Vc )
Fazendo t = 5.R.C temos :
5.R.C = R.C.ln( Vcc / Vc )
ln( Vcc / Vc ) = 5
Vcc / Vc = e^5
Vc = Vcc / e^5
e = 2,72
Vc = Vcc/148,9
Vc = 0,007.Vcc
Vc = 0,7 % Vcc
Para t = 5.R.C o capacitor perde 99,3 % de sua carga inicial.
t = R.C.ln(Vcc/(Vcc - Vc)) ( 1 )
t = RC(ln(Vcc/Vc)) ( 2 )
Fazendo ( 1 ) = ( 2 ) temos :
R.C.ln(Vcc/(Vcc - Vc)) = R.C.ln(Vcc/Vc)
ln(Vcc/(Vcc - Vc)) = ln(Vcc/Vc)
Vcc/(Vcc - Vc ) = Vcc/Vc
1/(Vcc - Vc) = 1 / Vc
Vc = Vcc - Vc
Vc + Vc = Vcc
2Vc = Vcc ( 3 )
Vc = Vcc/2
Vc = 0,50.Vcc
Vc = 50 % de Vcc
Levando ( 3 ) em ( 2 ) temos :
t = R.C.ln( 2Vc/Vc )
t = R.C.ln 2
t = 0,693.R.C
Energia armazenada em um capacitor carregado.
W = Energia armazenada em Joules.
C = Capacitância em Farads.
V = Diferença de potencial em Volts.
Física do Científico e do Vestibular. Vol 5 - Dalton Gonçalves
Física II - 1 - Halliday - Resnick